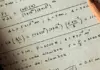Die Rücksubstitution bezeichnet einen Berechnungsprozess in der Mathematik, bei dem ermittelt wird, welche Werte man für bestimmte Variablen angeben muss, um eine gewisse Gleichung zu lösen. Der Name rührt daher, dass die ursprünglich eingesetzten Variablen häufig rückgängig gemacht werden, sodass die Gleichung gelöst werden kann.
Wie funktioniert die Rücksubstitution?
Zunächst wird die Gleichung so umgestellt, dass eine Unbekannte links steht. Die andere Unbekannte erscheint nun rechts von dem Gleichheitszeichen. Nun löst man die Gleichung und substituiert die erste Unbekannte in die linke Seite. Diese Operation wiederholt man mit der zweiten Unbekannten.
Worum geht es bei der Rücksubstitution?
Die Rücksubstitution ist eine Methode zum Lösen von linearen Gleichungssystemen. Bei dieser Methode wird der Wert der letzten Gleichung in die vorhergehende Gleichung eingesetzt und die Variable in dieser Gleichung gelöst. Sobald der Wert für diese Variable bekannt ist, wird er wieder in die vorhergehende Gleichung eingesetzt, und so weiter, bis alle Variablen bekannt sind.
Welche Vor- und Nachteile hat Rücksubstitution?
Es gibt viele Situationen, in denen Rücksubstitution eine schnelle und einfache Lösung bietet. Dabei wird die ursprünglich berechnete Gleichung umgestellt und so zu einer neuen Gleichung, aus der sich die gewünschte Lösung direkt ergibt.
Bei komplizierteren Aufgabenstellungen kann dieser Vorgang durch mehrere Rücksubstitutionen vereinfacht werden.
Die Vorteile von Rücksubstitution liegen auf der Hand: Sie ermöglicht die Lösung komplizierter Gleichungen, sie spart Zeit beim Lösen von Mathematikaufgaben und hilft bei der Überprüfung von gefundenen Lösungen.
Wie kann man die Rücksubstitution durchführen?
Ein sehr simples Beispiel für Rücksubstitution in der Mathematik ist die Umkehrung der Subtraktion.
Im Folgenden soll 7 – 5 = 2 berechnet werden.
Subtraktion: 7 – 5 = 2
Rücksubstitution: 2 + 5 = 7
Rücksubstitution bei einem Gleichungssystemen
Erklärung anhand von 5 Beispiel-Aufgaben:
Beispiel 1
Lösen Sie x in 2x + y = 5 und 3x – y = 8
Der erste Schritt besteht darin, beide Gleichungen so umzuschreiben, dass sich alle Variablen auf einer Seite des Gleichheitszeichens befinden:
Aus 2x + y = 5 wird 2x = -y + 5 und aus 3x -y = 8 wird 3x = -2y + 8.
Der zweite Schritt besteht darin, y zu lösen, indem man von jeder Seite von 2x = -y + 5 5 abzieht:
y = -7/2
Setzt man diesen Wert in eine der beiden ursprünglichen Gleichungen ein, so erhält man x wie gewünscht.
Wenn wir zum Beispiel y = -7/2 in 3x – y = 8 einsetzen, erhalten wir:
3(3) – (-7)/2) = 9 + 7/2 = 16 1/2
Was mit unserem ursprünglichen Lösungsverfahren übereinstimmt
Beispiel 2
In der Gleichung y = x-3 ist y die Abweichung von x in Grad und x der Ursprung.
Bestimme den Schnittpunkt von y = 0 mit dieser Geraden.
Der Schnittpunkt von y = 0 mit dieser Geraden liegt bei (3,0)
Beispiel 4
Weiß man, dass in der Gleichung y = ax + b die Zahl a steht für die Steigung und b für den y-Achsenabschnitt des Graphen von y = x, so kann man durch Einsetzen von x = 0 ermitteln, wo dieser Schnittpunkt liegt.
Bei der Rücksubstitution setzt man statt a nun die gesuchte Steigung und statt b den entsprechenden y-Achsenabschnitt ein. Die Lösung lautet also:
(0; -b)
Beispiel 4
Es soll herausgefunden werden, ob die Gleichung 3x + 7y = 6 stimmt oder nicht.
Dazu wird zunächst versucht, sie umzuformulieren.
Aus 3x + 7y = 6 folgt 3x – 6y = 0 und somit ist diese Gleichung linearisierbar.
Nun wird sie in die Gegenkathete überführt (soweit möglich), indem vor allem alle Terme mit y auflöst beziehungsweise abzieht (dabei bleiben Terme mit x erhalten):
3x – 6y = 0 -> 3x = 6y+0 -> y = -3/2x + 3/2
Das bedeutet jetzt aber noch nicht unbedingt, dass unsere ursprüngliche Gleichung stimmt!
Um das festzustellen, überprüft man nun bei unserer gegebenen linearen Gleichung den Nullpunktsatz
( mal -1):
(-1;3)
Hieraus ergibt sich , also stimmt unsere Ausgangsgleichheit!

Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)
Unsere Dienstleistungen:
-

Online Hausaufgabenhilfe in Mathe 1 Std.
100.00€ Add to cart -

Online Hausaufgabenhilfe in Physik 1 Std.
100.00€ Add to cart -

Online Nachhilfe in Mathe 11-13. Klasse 1 Std.
130.00€ Add to cart -

Online Nachhilfe in Mathe 5-10. Klasse 1 Std.
100.00€ Add to cart -

Online Nachhilfe in Physik 11-13. Klasse 1 Std.
130.00€ Add to cart -

Online Nachhilfe in Physik 5-10. Klasse 1 Std.
100.00€ Add to cart