Jeder, der in der Schule war, musste sich schon einmal damit herumschlagen, der Berechnung einer Querschnittsfläche. Den einen wird es leicht gefallen sein, den anderen ist und bleibt das Thema ein Rätsel. Aber Mathe ist kein Hexenwerk, wenn man es richtig angeht. Denn wenn man es einmal richtig verstanden hat, ist es ein Kinderspiel.
Zuerst einmal muss man wissen, was eine Querschnittsfläche ist. Da die Querschnittsfläche in das Gebiet der Geometrie fällt, wird hier die Fläche berechnet, die entsteht, wenn man einen Körper, welchen auch immer, von oben nach unten senkrecht zur Länge durchschneiden würde und dann aufklappt. Die dann sichtbar werdende Fläche nennt man Querschnittsfläche.
Formeln:
1)
Zur Berechnung der Querschnittsfläche eines Zylinders, welche kreisförmig ist, benötigt man den Radius (die Hälfte des Durchmessers) oder den Durchmesser. Die Querschnittsfläche trägt das Formelzeichen A und wird mit folgender Formel berechnet:
A = Pi * r² oder A = Pi *d
Das Ergebnis ist immer in mm², cm², dm² oder m².
Wenn man die Querschnittsfläche eines halben Zylinders berechnen möchte, lautet die Formel:
A = 1/2 * ( Pi * r² ), also genau die Hälfte der Kreisflächenformel.
Als Beispiel:
a) Berechnen Sie die Querschnittsfläche eines Baumes, welcher einen Radius von 48cm hat.
Rechnung: A = 3,14 * 48cm² = 2304 cm² oder 0,2304 m²
Antwort: Die Querschnittsfläche des Baumes beträgt 0,2304 m².
b) Berechnen Sie die Querschnittsfläche des halben Rohres mit einem Durchmesser von 30 cm hat.
Rechnung: A = 1/2 * ( 3,14 * 15cm² ) = 112,5 cm²
Antwort: Die Querschnittsfläche des halben Rohres beträgt 112,5 cm².
2)
Um die Querschnittsfläche eines Würfels, welches ein Quadrat bildet, zu berechnen, welches die wohl einfachste Variante der Querschnittsberechnung ist, benötigt man lediglich die Breite und die Länge des Quadrats. Die gleiche Formel gilt auch für die Querschittsfläche eines Quaders.
Auch hier trägt die Querschnittsfläche das Formelzeichen A. Die Formel lautet:
A = a * b , das bedeutet, man muss einfach die Breite mit der Länge multiplizieren und erhält somit die Querschnittsfläche.
Als Beispiel:
Würfel:
Berechnen Sie die Querschnittsfläche eines Würfels, mit einer Seitenlänge von 4,5cm.
Rechnung: A = 4,5cm² = 20,25 cm²
Antwort: Die Querschnittsfläche des Würfels beträgt 20,25 cm².
Quader:
Berechnen Sie die Querschnittsfläche eines Quaders mit der Seitenlänge a= 6 cm und der Seitenlänge b= 7,2 cm.
Rechnung: A = 6 cm * 7,2 cm = 43,2 cm²
Antwort: Die Querschnittsfläche des Quaders beträgt 43,2 cm².
3)
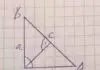
Um die Querschittsfläche eines Trapez zu berechnen, bedarf es schon etwas mehr mathematisches Verständnis.
Es werden beide Seitenlängen a und c benötigt und die Höhe h. Auch hier ist das Formelzeichen für die Querschittsfläche A.
Die Formel für die Berechnung lautet:
A = 1/2 * ( a+c ) * h
Als Beispiel:
Berechnen Sie die Querschittsfläche von einem Trapez mit den Seitenlängen a = 5 cm, c = 7 und der Höhe 4,5 cm.
Rechnung: A = 1/2 * ( 5 cm + 7 cm ) * 4,5 = 27 cm²
Antwort: Die Querschittsfläche des Trapez beträgt 27 cm².
Es wurden hier die gängigsten Querschnittsberechnungen behandelt, natürlich gibt es noch andere, vor allem zusammengesetzte Körper, wo eventuell zwei verschiedene Formeln gemeinsam verwendet werden müssen.
Man muss den Körper analysieren und versuchen, ihn so einfach wie möglich in einzelne Körper, dessen Querschittsflächen leicht zu berechnen sind, einzuteilen.
Viel Spaß beim Üben.
Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)
