In diesem Text beschäftigen wir uns mit der mathematischen Nutzung von Matrizen und wir möchten euch die Grundlagen vermitteln.
Die notwendigen Vorkenntnisse
Ich hoffe, dass sich viele von Euch noch an lineare Gleichungssysteme und die Aufgaben dazu erinnern. Wer davon nichts mehr weiß, sollte im Vorfeld sein Gedächtnis diesbezüglich noch einmal auffrischen. Wer sich jedoch erinnert, der weiß, dass das schriftliche Bearbeiten dieser Aufgaben sehr aufwändig ist, wenn das Gleichungssystem sehr groß war. Dies hatte auch den Nachteil, dass sich bei der ganzen Schreibarbeit Flüchtigkeitsfehler einschlichen.
Was ist eine Matrix?
Mithilfe einer Matrix lassen sich so große Aufgaben sehr viel schneller und einfacher lösen ,wenn man versteht, wie diese funktioniert.
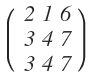
- Die Zeilen der Matrix sind sogenannte m-Zeilen. Das m bezeichnet die Zahl der Werte welche untereinander stehen. Man nennt die Zeilen einer solchen Matrix auch Zeilenvektoren.
- Die Spalten der Matrix sind sogenannte n-Zeilen. Das n bezeichnet die Zahl der Werte welche nebeneinander stehen. Und diese nennt man dann auch Spaltenvektoren. Also besitzt eine Matrix m * n Werte.
- Wenn eine Matrix lediglich eine Spalte besitzt, nennt man sie Spaltenmatrix. Besitzt sie lediglich eine Zeile, nennt man sie folglich Zeilenmatrix.
- a ik (ik tief stehend) nennt man Matrixelement.
Beispiele für Matrizen
Hier liefern wir euch einige Beispiele, indem wir euch zwei mal eine Matrix aufgeschrieben haben:
Beispiel 1
Das nachfolgende Beispiel hilft euch hoffentlich besser zu verstehen, wie der Aufbau einer Matrix gestaltet ist. Schaut euch dieses Beispiel genau an und versucht unsere Erklärung unter dem Bild nachzuvollziehen.
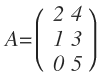
Wie ihr sehen könnt, besitzt diese Matrix drei Zeilen und zwei Spalten. Seine Elemente werden wie folgt bezeichnet: a11= 2 , a12= 4, a21 =1, a22= 3, a31= 0 und a32= 5.
Beispiel 2
Hier haben wir noch ein zweites Beispiel für euch, diesmal etwas komplexer:
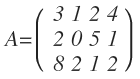
Wie ihr sehen könnt, besitzt diese Matrix immer noch drei Zeilen, aber die Spalten haben sich um zwei zusätzliche Spalten erweitert. Seine Elemente werden nun so bezeichnet: a11= 3, a12= 1, a13= 2, a14= 4, a21= 2, a22= 0, a23= 5, a24= 1, a31= 8, a32= 2, a33= 1 und a34= 2.

Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)
Unsere Dienstleistungen:
-

Online Hausaufgabenhilfe in Mathe 1 Std.
100.00€ Add to cart -

Online Hausaufgabenhilfe in Physik 1 Std.
100.00€ Add to cart -

Online Nachhilfe in Mathe 11-13. Klasse 1 Std.
130.00€ Add to cart -

Online Nachhilfe in Mathe 5-10. Klasse 1 Std.
100.00€ Add to cart -

Online Nachhilfe in Physik 11-13. Klasse 1 Std.
130.00€ Add to cart -

Online Nachhilfe in Physik 5-10. Klasse 1 Std.
100.00€ Add to cart