Was ist die Potenz von 2? – Berechnung

Einleitung

Potenzen sind ein fundamentales Konzept in der Mathematik, das uns hilft, große Zahlen auf eine kompakte und verständliche Weise darzustellen. Wenn wir von der „Potenz von 2“ sprechen, beziehen wir uns auf die Zahl 2, die eine bestimmte Anzahl von Malen mit sich selbst multipliziert wird. Dies wird durch den Exponenten angezeigt, der über der Basis (in diesem Fall 2) steht.

Kurze Einführung in das Thema Potenzierung

Die Potenzierung ist eine mathematische Operation, bei der eine Zahl, die als „Basis“ bezeichnet wird, eine bestimmte Anzahl von Malen mit sich selbst multipliziert wird. Der Exponent gibt an, wie oft die Basis mit sich selbst multipliziert wird. Zum Beispiel bedeutet , dass die Zahl 2 dreimal mit sich selbst multipliziert wird: .

Direkte Antwort auf die Frage: „Was ist die Potenz von 2?“

Die Potenz von 2 bezieht sich auf das Ergebnis der Multiplikation der Zahl 2 mit sich selbst für eine bestimmte Anzahl von Malen, die durch den Exponenten angegeben wird. Zum Beispiel ist die Potenz von 2 mit einem Exponenten von 3, also , gleich 8, da . Je nachdem, welcher Exponent verwendet wird, kann das Ergebnis variieren. So ist , und so weiter.

Grundlagen der Potenzierung

Die Potenzierung, auch als Exponentiation bekannt, ist eine der grundlegenden arithmetischen Operationen in der Mathematik. Sie ermöglicht es uns, eine Zahl schnell und effizient mit sich selbst zu multiplizieren, indem wir einen Exponenten verwenden. Dieser Abschnitt wird die Schlüsselkonzepte der Potenzierung vertiefen und ihre Anwendung mit der Basis 2 demonstrieren.

Definition von Potenzierung

Potenzierung ist der Prozess, bei dem eine Zahl (die Basis) eine bestimmte Anzahl von Malen mit sich selbst multipliziert wird. Der Exponent gibt an, wie oft diese Multiplikation stattfindet. Mathematisch ausgedrückt, wenn die Basis und der Exponent ist, dann ist die Potenz das Ergebnis von multipliziert mit sich selbst Mal.

Erklärung der Symbole und Termini: Basis, Exponent

Die Basis ist die Zahl, die wiederholt mit sich selbst multipliziert wird. Im Kontext dieses Artikels ist unsere Basis die Zahl 2. Der Exponent gibt an, wie oft die Basis mit sich selbst multipliziert wird. Zum Beispiel, in der Potenz , ist 2 die Basis und 3 ist der Exponent.

Beispiel mit der Basis 2

Um das Konzept der Potenzierung zu veranschaulichen, betrachten wir die Basis 2. Wenn wir einen Exponenten von 3 verwenden, erhalten wir . Dies bedeutet, dass wir 2 dreimal mit sich selbst multiplizieren: . Daher ist . Auf ähnliche Weise ist .

Berechnung der Potenz von 2

Die Berechnung der Potenz von 2 ist ein einfacher Prozess, der die wiederholte Multiplikation der Zahl 2 mit sich selbst beinhaltet. Je nachdem, welchen Exponenten wir verwenden, erhalten wir unterschiedliche Ergebnisse. In diesem Abschnitt werden wir uns ansehen, wie man die Potenz von 2 für verschiedene Exponenten berechnet und eine Referenztabelle für schnelle Konsultationen bereitstellen.

Schritt-für-Schritt-Anleitung zur Berechnung von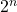

Um die Potenz von 2 für einen gegebenen Exponenten zu berechnen, führen Sie die folgenden Schritte aus:

1. Beginnen Sie mit der Zahl 1 als Ihr Startwert.
2. Multiplizieren Sie diesen Wert mit 2.
3. Wiederholen Sie die Multiplikation 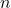Mal.
4. Das Ergebnis nach 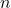Multiplikationen ist .

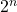Tabelle mit den Potenzen von 2 bis 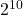für schnelle Referenz

Exponent	Ergebnis
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1024

Hinweis auf die exponentielle Zunahme der Ergebnisse

Wie aus der obigen Tabelle ersichtlich, wächst das Ergebnis exponentiell mit jedem zusätzlichen Schritt in der Potenzierung. Dies bedeutet, dass selbst kleine Erhöhungen des Exponenten zu erheblichen Steigerungen des Ergebnisses führen können. Dieses exponentielle Wachstum ist ein charakteristisches Merkmal der Potenzierung und ist besonders bei der Basis 2 deutlich sichtbar.

Anwendungen und Bedeutung der Potenzen von 2

Die Potenzen von 2 sind nicht nur ein interessantes mathematisches Konzept, sondern spielen auch in vielen wissenschaftlichen, technologischen und alltäglichen Anwendungen eine entscheidende Rolle. In diesem Abschnitt werden wir einige der wichtigsten Anwendungen und die Bedeutung der Potenzen von 2 in verschiedenen Bereichen untersuchen.

Verwendung in der Informatik (Binärsystem)

Das Binärsystem, das die Grundlage für die meisten modernen Computer bildet, verwendet nur zwei Ziffern: 0 und 1. Die Potenzen von 2 sind daher von zentraler Bedeutung für die Darstellung und Verarbeitung von Daten in Computern. Jedes Bit in einem Binärcode entspricht einer Potenz von 2, und die Kombination dieser Bits ermöglicht es Computern, eine Vielzahl von Informationen zu speichern und zu verarbeiten.

Relevanz in der Mathematik und Naturwissenschaften

In der Mathematik helfen die Potenzen von 2 bei der Lösung komplexer Probleme, insbesondere in Bereichen wie der Algebra und der Zahlentheorie. In den Naturwissenschaften, insbesondere in der Physik, werden Potenzen von 2 verwendet, um Phänomene wie die Interferenz von Wellen oder die Verteilung von Energie in Systemen zu beschreiben.

Beispiele aus dem Alltag, in denen Potenzen von 2 eine Rolle spielen

Die Potenzen von 2 begegnen uns auch im täglichen Leben. Ein gängiges Beispiel ist die Speicherkapazität von digitalen Speichermedien wie USB-Sticks oder Festplatten, die oft in Potenzen von 2 angegeben wird (z.B. 256 GB, 512 GB). Ein weiteres Beispiel ist die Berechnung von Zinseszinsen in der Finanzwelt, bei der Potenzen verwendet werden, um das Wachstum von Investitionen über die Zeit zu modellieren.

Häufig gestellte Fragen

Im Laufe der Zeit haben viele Menschen Fragen zur Potenz von 2 und ihrer Bedeutung gestellt. In diesem Abschnitt werden wir einige der am häufigsten gestellten Fragen zu diesem Thema beantworten, um ein tieferes Verständnis zu ermöglichen.

Warum ist die Potenz von 2 in der Informatik so wichtig?

In der Informatik basiert alles auf dem Binärsystem, einem System, das nur zwei Zustände kennt: 0 und 1. Diese binäre Darstellung entspricht den Potenzen von 2. Jedes zusätzliche Bit in einem Computer verdoppelt die Anzahl der möglichen Zustände, was durch die Potenzen von 2 repräsentiert wird. Daher sind die Potenzen von 2 grundlegend für die Funktionsweise von Computern und digitalen Systemen.

Wie berechnet man die Potenz einer anderen Zahl?

Die Potenz einer Zahl wird berechnet, indem man die Basis (die Zahl selbst) so oft mit sich selbst multipliziert, wie es der Exponent angibt. Zum Beispiel: Für multipliziert man die Zahl 3 viermal mit sich selbst: .

Was ist der Unterschied zwischen Potenz und Wurzel?

Während die Potenzierung das wiederholte Multiplizieren einer Zahl mit sich selbst darstellt, ist die Wurzel das genaue Gegenteil. Die Wurzel einer Zahl versucht herauszufinden, welche Zahl, wenn sie eine bestimmte Anzahl von Malen mit sich selbst multipliziert wird, das gegebene Ergebnis liefert. Zum Beispiel ist die Quadratwurzel von 9 gleich 3, weil .

Anatoli Bauer

Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)