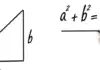Wieviel Grad hat ein Dreieck? – Aufklärung

Das Dreieck ist eine geometrische Figur und kommt im Wesentlichen in der Trigonometrie, einem Teilbereich der Mathematik, zum Einsatz. Der Dreiecksgeometrie wird in der Mathematik ein ganzes Kapitel zugeordnet. Obwohl es sich um eine der einfachsten Geometriefiguren handelt, ist das Dreieck aufgrund seiner Variablen in der Trigonometrie bedeutend. Das Synonym zum Dreieck heißt Triangel vom lateinischen Triangulum.

Merkmale eines Dreiecks

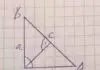
Das Dreieck wird von drei geraden Linien begrenzt. Die drei äußeren Punkte der geometrischen Figur werden Eckpunkte genannt. Innen ergeben sich drei Innenwinkel. Den Winkeln und Seiten werden in der Mathematik arabische und griechische Buchstaben zugeordnet, die der Berechnung der Längen und Winkelgrade dienen.

Zunächst gilt es, das allgemeine Dreieck zu verstehen, bevor man sich mit der Eingangsfrage, bezogen auf weitere Dreiecksvarianten, beschäftigt. In einem ebenen Dreieck beträgt die Gesamtsumme aller drei Innenwinkel immer 180 Grad. Demnach ergibt ein Innenwinkel eines Dreiecks 60 Grad. Das Dreieck verfügt im Äußeren über zwei Scheitelwinkel, die die Grundsumme aller äußeren Winkel von 360 Grad verdoppeln, woraus sich insgesamt 720 Grad ergeben. In der Mathematik wird das nur fachspezifisch angewandt.

Einteilung der Dreiecke

Vom allgemeinen oder ebenen Dreieck gibt es weitere Dreiecksvarianten, die nach ihrer Seitenlänge oder Winkelgröße geordnet werden.

Das unregelmäßige Dreieck basiert auf drei unterschiedliche Seitenlängen und somit auch drei unterschiedlichen Winkeln.

Das gleichschenklige Dreieck setzt voraus, dass mindestens zwei Seitenlängen identisch lang sind. Daraus ergeben sich zwei gleichgroße Innenschenkel oder auch Innenwinkel genannt.

Das regelmäßige oder gleichseitige Dreieck mit 180 Grad als Summe aller Innenwinkel verfügt über drei gleichlange Seiten. Es ist eine der häufigsten geometrischen Figuren.

Das rechtwinklige Dreieck beinhaltet einen rechten Winkel. Ein rechter Winkel ist immer einer von vier Teilen eines vollen Winkels mit 360 Grad und misst 90 Grad. Die gegenüberliegende Seite des rechten Winkels wird in der Mathematik als Hypotenuse bezeichnet.

Das spitzwinklige Dreieck ist daran zu erkennen, dass alle Winkel kleiner als 90 Grad sind. Das bedeutet aber nicht, dass zwingend alle Seitenlängen gleichgroß sein müssen.

Das stumpfwinklige Dreieck setzt sich aus einem Winkel zwischen 90 und 180 Grad und zwei spitzen Winkeln unter 90 Grad zusammen.

Wie groß die jeweiligen Winkel eines Dreiecks sind, lässt sich nur bedingt ohne Berechnung bestimmen. Als Dreieck gilt alles, was durch drei Seiten miteinander verbunden ist und eine messbare Innenfläche bietet. Die Seitenlängen sind dabei variabel. Es gibt außerdem auch außerhalb der euklidischen Geometrie Dreiecke.

Sphärische und hyperbolische Dreiecke

Das sphärische Dreieck wird durch drei Seiten, die sich aus Kreisen ergeben, begrenzt. Alternativ ist das sphärische Dreieck unter Kugeldreieck bekannt. Die einzelne Winkelgröße beträgt beim sphärischen Dreieck mindestens 180 Grad. Die Summe aller Winkel beträgt demnach mindestens 540 Grad. Die Längen werden nicht im Längenmaß gemessen, da das Dreieck aus sich kreuzenden Linien dreier Kreise ergibt.

Hyperbolische Dreiecke bilden sich unter anderem auf Satteln. Sie zeichnen sich dadurch aus, dass jeder Winkel kleiner als 180 Grad ist.

Anatoli Bauer

Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)