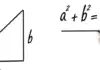Das Dreieck ist eine der grundlegendsten und am häufigsten vorkommenden geometrischen Formen in der Mathematik und im täglichen Leben. Ob in der Architektur, im Design oder in der Natur – Dreiecke sind überall zu finden. Eine der häufigsten Fragen, die sich bei der Betrachtung eines Dreiecks stellt, ist die nach seinem Flächeninhalt. Wie berechnet man den Flächeninhalt eines Dreiecks? Diese Frage mag auf den ersten Blick einfach erscheinen, insbesondere wenn man an das rechtwinklige Dreieck denkt. Doch es gibt verschiedene Methoden und Formeln, je nachdem, welche Informationen über das Dreieck bekannt sind.
Grundlagen
Dreiecke sind dreiseitige Polygone, die in der Geometrie eine zentrale Rolle spielen. Sie können auf verschiedene Arten klassifiziert werden, je nach ihren Seitenlängen und Innenwinkeln. Diese Klassifikation hilft uns, die richtige Methode zur Berechnung des Flächeninhalts zu wählen.
Definition eines Dreiecks und seiner Eigenschaften
Ein Dreieck ist eine geometrische Form, die aus drei geraden Seiten besteht, die sich in drei Punkten schneiden. Diese Punkte werden als die Eckpunkte des Dreiecks bezeichnet. Die Seitenlänge eines Dreiecks und die Größe seiner Innenwinkel sind die Hauptfaktoren, die seine Form und Eigenschaften bestimmen.
Unterscheidung zwischen verschiedenen Arten von Dreiecken
Es gibt verschiedene Arten von Dreiecken, basierend auf den Längen ihrer Seiten und ihren Innenwinkeln:
- Gleichseitiges Dreieck: Alle drei Seiten sind gleich lang und alle Innenwinkel messen 60 Grad.
- Gleichschenkliges Dreieck: Zwei Seiten sind gleich lang und die Winkel gegenüber diesen Seiten sind gleich groß.
- Rechtwinkliges Dreieck: Einer der Innenwinkel misst genau 90 Grad.
- Spitzwinkliges Dreieck: Alle Innenwinkel sind kleiner als 90 Grad.
- Stumpfwinkliges Dreieck: Einer der Innenwinkel ist größer als 90 Grad.
Die Kenntnis der spezifischen Art des Dreiecks ermöglicht es uns, die am besten geeignete Methode zur Berechnung seines Flächeninhalts zu wählen.
Flächenberechnung bei einem rechtwinkligen Dreieck
Das rechtwinklige Dreieck ist eine der bekanntesten Dreiecksformen. Es zeichnet sich durch einen Winkel von genau 90 Grad aus. Die beiden Seiten, die den rechten Winkel bilden, werden als Katheten bezeichnet, während die gegenüberliegende Seite, die längste Seite, als Hypotenuse bekannt ist.
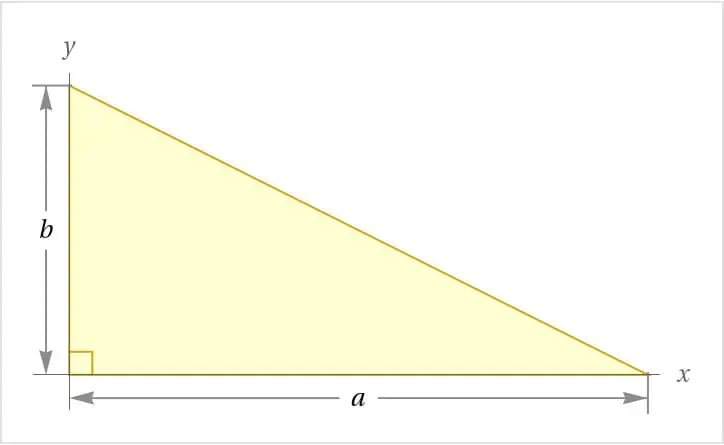
Formel: Flächenberechnung eines rechtwinkligen Dreiecks
Die Fläche eines rechtwinkligen Dreiecks kann einfach mit der folgenden Formel berechnet werden:
![\[ A = \frac{1}{2} \times a \times b \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-9ea11170dec215e809400e14a230933e_l3.png "Rendered by QuickLaTeX.com")
Hierbei sind 
und 
die Längen der beiden Katheten des Dreiecks. Diese Formel basiert auf der Tatsache, dass die Fläche eines Rechtecks die Multiplikation seiner Länge und Breite ist, und da ein rechtwinkliges Dreieck die Hälfte eines Rechtecks ist, teilen wir das Produkt der Katheten durch zwei.
Beispiel: Flächenberechnung eines rechtwinkligen Dreiecks
Angenommen, ein rechtwinkliges Dreieck hat Katheten von 6 cm und 8 cm Länge. Die Fläche dieses Dreiecks kann wie folgt berechnet werden:
![\[ A = \frac{1}{2} \times 6 \, \text{cm} \times 8 \, \text{cm} = 24 \, \text{cm}^2 \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-cfedf74b63522ea9b00e34c96edab2e9_l3.png "Rendered by QuickLaTeX.com")
Dies gibt uns den Flächeninhalt des rechtwinkligen Dreiecks basierend auf den gegebenen Katheten.
Flächenberechnung bei einem Dreieck ohne rechten Winkel
Während rechtwinklige Dreiecke ihre eigene spezifische Formel für die Flächenberechnung haben, benötigen Dreiecke ohne rechten Winkel eine andere Herangehensweise. Eine solche Methode nutzt den Sinus des eingeschlossenen Winkels zwischen zwei Seiten des Dreiecks.
Formel für die Flächenberechnung mithilfe des Sinus
Die Fläche eines Dreiecks, das keinen rechten Winkel hat, kann mit der folgenden Formel berechnet werden:
![\[ A = \frac{1}{2} \times a \times b \times \sin(\gamma) \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-3e88cb5cd730a2b03921c8f450d035a1_l3.png "Rendered by QuickLaTeX.com")
Hierbei sind und zwei beliebige Seiten des Dreiecks und 
ist der Winkel zwischen diesen beiden Seiten. Diese Formel nutzt die trigonometrische Funktion des Sinus, um den Flächeninhalt des Dreiecks zu bestimmen.
Beispiel: Flächenberechnung mithilfe des Sinus
Angenommen, ein Dreieck hat die Seitenlängen 
und 
und der eingeschlossene Winkel beträgt 60 Grad. Die Fläche dieses Dreiecks kann wie folgt berechnet werden:
![\[ A = \frac{1}{2} \times 5 \, \text{cm} \times 7 \, \text{cm} \times \sin(60^\circ) \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-c98bdfeac0f4e151a935de937b1cd5e0_l3.png "Rendered by QuickLaTeX.com")
Um den genauen Wert zu erhalten, kann man den Sinus von 60 Grad berechnen und in die Formel einsetzen.
Flächenberechnung mit Hilfe des Heronschen Formels
Die Heronsche Formel bietet eine weitere Methode zur Berechnung des Flächeninhalts eines Dreiecks, basierend auf den Längen aller drei Seiten. Diese Formel ist besonders nützlich, wenn die Höhe des Dreiecks nicht bekannt ist oder wenn das Dreieck keine besonderen Eigenschaften wie einen rechten Winkel aufweist.
Herleitung der Heronschen Formel
Die Heronsche Formel wurde nach dem antiken griechischen Mathematiker Heron von Alexandria benannt. Die Formel verwendet den sogenannten Halbumfang des Dreiecks, der als 
bezeichnet wird und wie folgt definiert ist:
![\[ s = \frac{a + b + c}{2} \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-ad47d0d625aa7a5140f5be2d4a74209a_l3.png "Rendered by QuickLaTeX.com")
Wobei , und 
die Längen der drei Seiten des Dreiecks sind. Mit diesem Halbumfang kann die Fläche 
des Dreiecks berechnet werden:
![\[ A = \sqrt{s(s-a)(s-b)(s-c)} \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-dfa8a60b2a50ae01cfe296a957ecb6a3_l3.png "Rendered by QuickLaTeX.com")
Beispiel: Flächenberechnung mit der Heronschen Formel
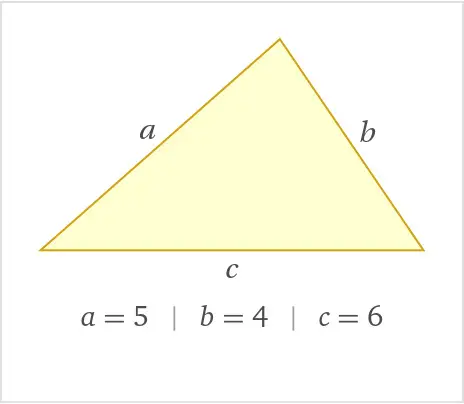
Angenommen, ein Dreieck hat die Seitenlängen , 
und 
. Zuerst berechnen wir den Halbumfang:
![\[ s = \frac{5 \, \text{cm} + 6 \, \text{cm} + 7 \, \text{cm}}{2} \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-03af048eeb382430e861bfd5ca669ffa_l3.png "Rendered by QuickLaTeX.com")
Mit dem ermittelten Wert für kann nun die Fläche des Dreiecks berechnet werden:
![\[ A = \sqrt{s(s-5 \, \text{cm})(s-6 \, \text{cm})(s-7 \, \text{cm})} \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-bb158a59d254cd18517a859d8266172d_l3.png "Rendered by QuickLaTeX.com")
Dies gibt uns den Flächeninhalt des Dreiecks basierend auf den gegebenen Seitenlängen.
Häufig gestellte Fragen
Bei der Betrachtung des Flächeninhalts von Dreiecken gibt es viele Fragen, die häufig gestellt werden. Hier sind einige der am häufigsten gestellten Fragen und ihre Antworten.
Wie berechnet man den Flächeninhalt eines gleichseitigen Dreiecks?
Ein gleichseitiges Dreieck ist ein Dreieck, bei dem alle drei Seiten gleich lang sind. Die Fläche eines gleichseitigen Dreiecks kann mit der folgenden Formel berechnet werden:
![\[ A = \frac{\sqrt{3}}{4} \times a^2 \]](https://mathe2go.net/wp-content/ql-cache/quicklatex.com-df693b63a4eb6b7af17d9089992bb4d5_l3.png "Rendered by QuickLaTeX.com")
Wobei die Länge einer Seite des Dreiecks ist.
Was ist der Unterschied zwischen Basis und Höhe in einem Dreieck?
Die Basis eines Dreiecks ist eine der Seiten, normalerweise die untere Seite, wenn das Dreieck gezeichnet wird. Die Höhe (oder Altitude) ist die senkrechte Entfernung von der Basis zu dem gegenüberliegenden Eckpunkt. Es ist wichtig zu beachten, dass die Höhe nicht immer eine der Seiten des Dreiecks ist, es sei denn, das Dreieck ist rechtwinklig.
Wie kann man den eingeschlossenen Winkel in einem Dreieck messen?
Der eingeschlossene Winkel in einem Dreieck ist der Winkel, der von zwei gegebenen Seiten des Dreiecks gebildet wird. Er kann mit einem Winkelmesser oder einem anderen geeigneten Instrument gemessen werden. In der Trigonometrie kann der Sinus, Kosinus oder Tangens des Winkels auch verwendet werden, um den Wert des Winkels zu bestimmen, wenn die Längen der Seiten bekannt sind.
Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)
