Prisma berechnen – Volumen, Oberfläche, Mantelfläche – Formeln, Beispiele

In dem Artikel geht es um das Thema: Prisma berechnen. Falls du ein paar Probleme mit dem Thema hast, solltest du den Text unbedingt weiter lesen. Erst einmal sollten wir klären, was ein Prisma überhaupt ist.

Ein Prisma ist wie folgt aufgebaut:

• – Es hat ein Vieleck als Grundfläche
• – Die Seitenkanten sind Parallel und gleich lang

Man unterscheidet zwischen dem schiefem Prisma und den geraden Prisma.
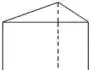
Die folgende Grafik zeigt ein gerades Prisma:

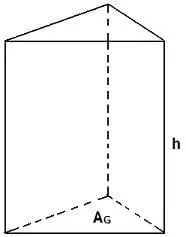
Formeln von einem Prisma

Natürlich benötigst du, wie für jeden Körper, bestimmte Formeln für das Prisma.
Wie die Formeln genau ausschauen, siehst du hier:

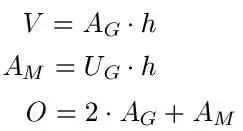
Falls du nicht genau weißt, was die Buchstaben genau bedeuten, wird das hier noch einmal aufgelistet:

• „V“ steht dabei für das Volumen
• „AG“ steht dabei für die Grundfläche
• „h“ steht dabei für die Höhe
• „AM“ steht für die Mantelfläche
• „UG“ steht für den Umfang der Grundfläche
• „O steht für die Oberfläche

Unterschied zwischen geradem und schiefem Prisma

Jedes Prisma hat, wie beschrieben, eine Grundfläche, ein Vieleck. Von dieser gehen gleich lange und zueinander parallele Kanten aus. Diese führen zur Deckenfläche, die mit der Grundfläche kongruent ist, also hinsichtlich Form und Maßen deckungsgleich mit der Grundfläche ist.
Stehen die parallelen Kanten, die die Höhe eines Prismas bestimmen, senkrecht auf dessen Grundfläche, handelt es sich um ein gerades Prisma.
Bei einem schiefen Prisma stehen die parallelen Kanten dagegen nicht senkrecht auf der Grundfläche, also nicht in einem 90-Grad Winkel zu dieser, sondern in einem von 90-Grad verschiedenen Winkel.

Volumen eines Prismas

Ein Prisma ist ein Körper. Jeder Körper hat ein Volumen. Beispiel: Marmeladengläser, die nicht rund sind, haben oft die Form eines Prismas mit Grundfläche und Deckenfläche, auf der quasi der Deckel sitzt. Marmeladengläser sind gefüllt, haben Volumen. Doch wie viel Luft, Wasser oder Marmelade passt in ein derartiges Beispielprisma hinein?

Formel für die Berechnung des Volumens eines Prismas: Grundfläche mal Höhe (siehe oben)

1. Berechnen der Grundfläche

Wichtig! Je nachdem, welche Form die Grundfläche des Prismas hat, zum Beispiel die eines Dreiecks oder Rechtecks, gilt es verschiedene Flächenberechnungsformeln anzuwenden, zum Beispiel:

Fläche rechtwinkliges Dreieck: A = 1/2 mal Grundseite g des Dreiecks mal Höhe des Dreiecks. A = g*h
Fläche Rechteck: A = Seitenlänge (a) des Rechtecks mal Seitenbreite des Rechtecks (b). A = a*b

2. Berechnen der Höhe.

Die Höhe des Prismas ist die Länge von dessen Kanten.

Beispielberechnung:

Prisma mit Grundfläche Quadrat (Seitenlängen jeweils 5 cm) und Kantenhöhe 10 cm.

Volumen = Grundfläche Quadrat * Kantenhöhe = 5 Zentimeter * 5 Zentimeter * 10 Zentimeter = 25 Quadratzentimeter * 10 Zentimeter = 250 Kubikzentimeter.

250 Kubikzentimeter entspricht übrigens 0,25 Liter. Ein Marmeladenglas mit den hier beispielhaft verwandten Maßen könnte daher mit maximal 0,25 Liter Wasser oder besser 250 ml oder 250 Gramm Marmelade befüllt werden.

Mantel eines Prismas.
Die Mantelfläche eines Prismas ist quasi die Oberfläche des Körpers ohne dessen Grundfläche und Deckenfläche.

Formel für die Berechnung der Mantelfläche: Umfang der Grundfläche mal Höhe des Prismas (siehe oben). Der Umfang der Grundfläche ist die Summe von deren Seitenlängen.

Beispielberechnungen:

1) Prisma mit Grundfläche Quadrat (Seitenlängen je 5 cm) und Kantenhöhe 10 cm.

Umgang der Grundfläche = 5 cm + 5cm + 5cm + 5cm = 20 cm. Höhe Prisma = 10 cm.

Mantelfläche Prismas = 20 Zentimeter * 10 Zentimeter = 200 Quadratzentimeter. Auf dieser Fläche hätte zum Beispiel die Banderole des oben beschriebenen Beispiel-Marmeladenglases Platz.

2) Prisma mit Grundfläche gleichseitiges Dreieck (Seiten je 5 cm) und Kantenhöhe 4 cm.

Umfang der Grundfläche = 5 Zentimeter + 5 Zentimeter + 5 Zentimeter. Höhe Prisma 4 cm.

Mantelfläche Prisma = 15 Zentimeter * 4 Zentimeter = 60 Quadratzentimeter

Oberfläche eines Prismas

Alle äußere Flächen eines Primas zusammengenommene machen seine Oberfläche aus. Diese
besteht demnach aus der Mantelfläche und zweimal der Grundfläche beziehungsweise einmal der
Grundfläche und einmal der Deckenfläche.

Die Oberfläche eines Prismas ist die Summe seiner Gesamtflächen.

Beispielberechnung:

1. Prisma mit Grundfläche Quadrat (Seitenlängen je 5 cm) und Kantenhöhe 10 cm.

Oberfläche = Mantelfläche ((5cm + 5cm + 5 cm + 5cm) * 10 cm) + Grundfläche Prisma (5cm * 5cm) + Deckenfläche Prisma (5cm * 5cm) = 200 Quadratzentimeter + 25 Quadratzentimeter + 25 Quadratzentimeter= 250 Quadratzentimeter.

Würde man das oben erwähnte Beispielprisma, das Marmeladenglas, in Geschenkpapier verpacken wollen, müsste genug Papier vorhanden sein, um damit 250 Quadratzentimeter bedecken zu können.

Anatoli Bauer

Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)