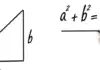In diesem Abschnitt wollen wir uns etwas näher mit dem Satz des Pythagoras beschäftigen, den man auch einfach unter der Formel a2 + b2 = c2 kennt. Es soll erklärt werden, wann der Satz des Pythagoras angewendet wird und wie man mit der Formel genau arbeitet.
Die Gleichung a2 + b2 = c2 ist den meisten einschlägig bekannt, selbst wenn die Schulzeit schon weit zurückliegt.
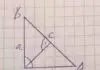
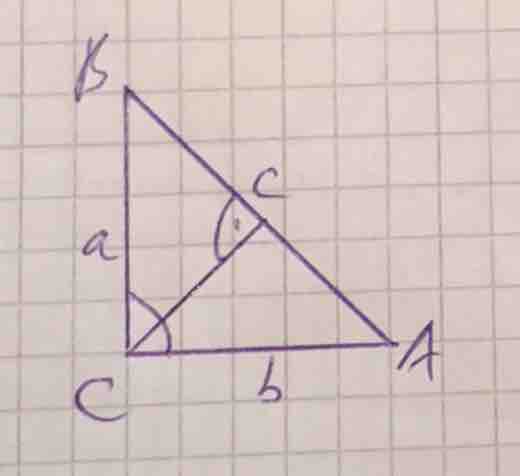
Anwendung findet diese Formel nur bei rechtwinkligen Dreiecken. Sie dient dazu, die längen der jeweiligen Seiten zu berechnen.
Dabei sind:
a und b die Längen der Katheten
c die Länge der Hypotenuse
Dabei ist zu beachten, dass alle Längen in der gleichen Einheit angegeben werden.
Anwenden von a2 + b2 = c2 mit Beispiele
je nachdem welche Seitenlänge des rechtwinkligen Dreiecks man berechnen will, muss man die Gleichung entweder nach a, b oder c umstellen. Daher soll hier erst einmal die allgemeine Formel entsprechend für jede Seite a, b oder c umgestellt werden. Dann ergibt sich aus a2 + b2 = c2:
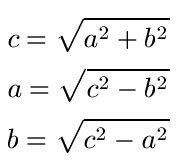
Anhand von einigen Beispielen wollen wir uns die Berechnung nun etwas näher anschauen.
Beispiel 1:
Gegeben sei: c = 10 cm, b =sei 5 cm. Wie lange ist a?
Lösung: Wir können direkt die angegebenen Zahlen in die Formel einsetzen. Es ist jedoch darauf zu achten, dass sowohl die Zahlen als auch die Einheiten quadriert werden müssen. Da am Ende aus dem errechneten Wert die Wurzel gezogen wird, haben wir wieder cm als Einheit.
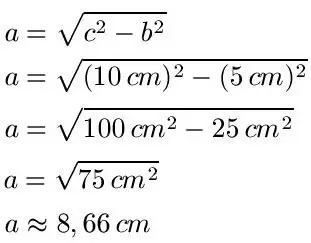
Beispiel 2:
gegeben a= 8 Meter, b = 30 cm. Wie lange ist die Hypotenuse c?
Lösung: Wir müssen alles in der gleichen Einheit einsetzen: 8m = 800cm. Danach Einsetzen in die Formel:
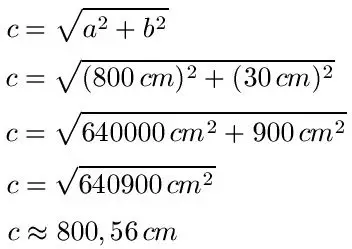
Der Satz des Pythagoras
Einführung
Im heutigen Artikel werden wir analysieren, was der Satz des Pythagoras ist, besser bekannt unter der Formel a^2+b^2=c^2.
Wir werden analysieren, was er ist, wo er herkommt und welche praktischen Anwendungen er für die Lösung von Geometrie- und Mathematikproblemen hat.
Was ist der Zweck des Satzes von Pythagoras?
Der Satz des Pythagoras ist eine mathematische Formel, mit der man die Seitenlängen eines rechtwinkligen Dreiecks berechnen kann.
Eine kurze Geschichte des Satzes von Pythagoras
Der Überlieferung nach wurde der Satz des Pythagoras von dem griechischen Philosophen und Mathematiker Pythagoras erfunden. Tatsächlich haben Historiker herausgefunden, dass diese mathematische Formel bereits etwa 1 000 Jahre zuvor von den Ägyptern entdeckt worden war, und anderen Quellen zufolge hatten die Babylonier bereits 4 000 Jahre zuvor eine sehr ähnliche Formel entdeckt.
Der Legende nach soll Pythagoras sein Theorem entwickelt haben, während er darauf wartete, von Polykrates empfangen zu werden. Pythagoras saß in einer großen Halle im Palast des Tyrannen von Samos, als ihm die quadratischen Fliesen auf dem Boden unter seinen Füßen auffielen. Durch Teilung der quadratischen Fliese in zwei gleiche rechtwinklige Dreiecke konnten zwei gleiche Dreiecke gebildet werden, und ein Quadrat, das durch Bauen auf der Diagonale eines dieser beiden rechtwinkligen Dreiecke entstand, war doppelt so groß wie eine einzelne Fliese.
In Wirklichkeit bestand dieses Quadrat aus vier halben Ziegeln, also zwei Ziegeln auf jeder Seite. Im Gegensatz dazu entsprachen die Quadrate, die auf den anderen Seiten des Dreiecks errichtet wurden, jeweils der Fläche einer einzelnen Keramikkachel. Das heißt, das auf der Hypotenuse gebildete Quadrat entspricht der Summe der auf den beiden anderen Seiten gebildeten Quadrate.
Der Legende nach kam Pythagoras bei dieser Begebenheit auf die Idee für sein Theorem, das wir heute alle in der Schule lernen.
Wie man den Satz des Pythagoras anwendet
Die Aussage des Satzes von Pythagoras lautet wie gesagt: a^2+b^2=c^2
A ist die Länge des Katheten Nummer 1
B ist die Länge der Kathete Nr. 2
C ist die Länge der Hypotenuse.
Wenn wir eine dieser drei Längen finden wollen, müssen wir eine dieser drei Formeln anwenden:
c= a^2 + b^2
a = c^2 – b^2
b= c^2 – a^2
Betrachten wir nun gemeinsam einige Beispiele für die Anwendung dieser Formeln.
Beispiel Nummer 1
a misst 10 cm
b misst 5 cm
Wie groß ist c?
In diesem Fall müssen wir diese Formel anwenden: c= a^2 + b^2
C= (10cm)^2 + (5cm)^2 = 11,18 cm
Beispiel Nummer 2
b ist 7 cm
c ist 12 cm
Wie viel misst a?
In diesem Fall müssen wir die zweite Formel anwenden, die wir gesehen haben: a = c^2 – b^2
a= (12cm)^2 – (7cm)^2 = 9,74 cm
Beispiel 3
a ist 2 cm
c ist 21 cm
Wie groß ist b?
In diesem Fall müssen wir die dritte Formel anwenden, die wir gesehen haben, nämlich: b= c^2 – a^2
b= (21cm)^2 – (2cm)^2 = 20,90 cm
Schlussfolgerung
In diesem Artikel haben wir genauer analysiert, was der Satz des Pythagoras ist, und versucht herauszufinden, was seine Geschichte ist, wer ihn entdeckt hat und wie er verwendet werden kann.
Die Anwendung des Satzes von Pythagoras ist nicht sehr schwierig, wichtig ist nur, dass man die drei grundlegenden Formeln auswendig lernt.
Wenn Sie Schwierigkeiten haben, sich die drei Formeln auswendig zu merken, können Sie diese drei Formeln aus der Ausgangsformel a^2+b^2=c^2 ableiten. Die drei Formeln, die wir dir gezeigt haben, sind nämlich die Umkehrformeln dieser Formel.
Viel Spaß beim Lernen!

Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)
Unsere Dienstleistungen:
-

Online Hausaufgabenhilfe in Mathe 1 Std.
100.00€ Add to cart -

Online Hausaufgabenhilfe in Physik 1 Std.
100.00€ Add to cart -

Online Nachhilfe in Mathe 11-13. Klasse 1 Std.
130.00€ Add to cart -

Online Nachhilfe in Mathe 5-10. Klasse 1 Std.
100.00€ Add to cart -

Online Nachhilfe in Physik 11-13. Klasse 1 Std.
130.00€ Add to cart -

Online Nachhilfe in Physik 5-10. Klasse 1 Std.
100.00€ Add to cart