Dreiecke sind eine der grundlegendsten und am häufigsten vorkommenden geometrischen Formen in der Mathematik und im täglichen Leben. Sie sind in Architektur, Design, Kunst und Natur allgegenwärtig. Die Berechnung des Flächeninhalts eines Dreiecks ist eine grundlegende Fähigkeit, die in vielen Bereichen, von der Schule bis zur Ingenieurwissenschaft, benötigt wird. Während die meisten von uns mit der Berechnung des Flächeninhalts eines rechtwinkligen Dreiecks vertraut sind, gibt es Situationen, in denen wir mit Dreiecken konfrontiert werden, die keinen rechten Winkel haben. In solchen Fällen benötigen wir eine andere Methode zur Berechnung des Flächeninhalts.
Direkte Anleitung: Flächeninhalt eines Dreiecks ohne rechten Winkel berechnen
Formel für den Flächeninhalt
Um den Flächeninhalt eines Dreiecks ohne rechten Winkel zu berechnen, benötigen wir eine spezielle Formel, die die Längen der beiden Seiten und den Sinus des eingeschlossenen Winkels verwendet. Die Formel lautet:
![]()
Wo:
 und
und 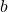 die Längen der beiden Seiten sind, die den Winkel
die Längen der beiden Seiten sind, die den Winkel 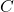 einschließen.
einschließen.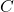 ist der eingeschlossene Winkel zwischen den Seiten
ist der eingeschlossene Winkel zwischen den Seiten  und
und 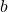 .
.
Schritt-für-Schritt-Anleitung zur Anwendung der Formel
- Messen Sie die Längen der beiden Seiten
 und
und 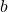 , die den eingeschlossenen Winkel
, die den eingeschlossenen Winkel 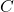 bilden.
bilden. - Messen oder berechnen Sie den Wert des eingeschlossenen Winkels
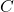 .
. - Verwenden Sie die Sinusfunktion, um den Sinuswert des Winkels
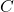 zu erhalten.
zu erhalten. - Setzen Sie die gemessenen Werte in die obige Formel ein, um den Flächeninhalt
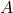 zu berechnen.
zu berechnen.
Ein praktisches Beispiel: Angenommen, Sie haben ein Dreieck mit den Seitenlängen ![]() cm und
cm und ![]() cm und einem eingeschlossenen Winkel von
cm und einem eingeschlossenen Winkel von ![]() . Der Flächeninhalt des Dreiecks kann mit der obigen Formel berechnet werden.
. Der Flächeninhalt des Dreiecks kann mit der obigen Formel berechnet werden.
Praktisches Beispiel
Gegeben:
 cm
cm cm
cm
Einsetzen in die Formel:
![]()
Um den genauen Wert für ![]() zu berechnen, können wir die Werte in die Formel einsetzen.
zu berechnen, können wir die Werte in die Formel einsetzen.
Das Ergebnis der Berechnung ist:
![]()
Das bedeutet, dass ein Dreieck mit den gegebenen Maßen einen Flächeninhalt von ungefähr ![]() hat.
hat.
Wichtige Begriffe und Konzepte
Dreieck: Definition und Arten von Dreiecken
Ein Dreieck ist eine geometrische Form, die aus drei geraden Seiten besteht, die sich in drei Ecken treffen. Jede Ecke wird als Winkel bezeichnet, und die Summe der drei Winkel in einem Dreieck beträgt immer ![]() . Es gibt verschiedene Arten von Dreiecken, basierend auf ihren Winkeln und Seiten:
. Es gibt verschiedene Arten von Dreiecken, basierend auf ihren Winkeln und Seiten:
- Spitzwinkliges Dreieck: Alle drei Winkel sind kleiner als
 .
. - Rechtwinkliges Dreieck: Ein Winkel ist genau
 .
. - Stumpfwinkliges Dreieck: Ein Winkel ist größer als
 .
.
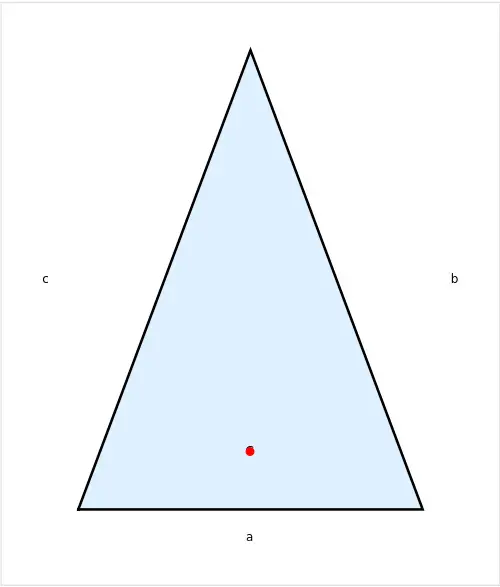
Sinus eines Winkels
Der Sinus eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der gegenüberliegenden Seite zur Länge der Hypotenuse. Mathematisch ausgedrückt, für einen Winkel ![]() :
:
![]()
Der Sinuswert variiert zwischen -1 und 1 und ist eine Schlüsselfunktion in der Trigonometrie, die in vielen Bereichen der Mathematik und Physik Anwendung findet.
Eingeschlossener Winkel: Definition und Bestimmung
Der eingeschlossene Winkel in einem Dreieck ist der Winkel, der von zwei gegebenen Seiten gebildet wird. In der Formel zur Berechnung des Flächeninhalts eines Dreiecks ohne rechten Winkel bezieht sich der eingeschlossene Winkel auf den Winkel, der von den Seiten ![]() und
und ![]() gebildet wird. Es ist wichtig, den korrekten eingeschlossenen Winkel zu verwenden, um genaue Ergebnisse bei der Berechnung des Flächeninhalts zu erzielen.
gebildet wird. Es ist wichtig, den korrekten eingeschlossenen Winkel zu verwenden, um genaue Ergebnisse bei der Berechnung des Flächeninhalts zu erzielen.
Praktische Beispiele
Beispiel 1: Berechnung des Flächeninhalts eines Dreiecks mit gegebenen Seitenlängen und eingeschlossenem Winkel
Angenommen, Sie haben ein Dreieck mit den Seitenlängen ![]() cm und
cm und ![]() cm und einem eingeschlossenen Winkel von
cm und einem eingeschlossenen Winkel von ![]() . Um den Flächeninhalt zu berechnen, verwenden Sie die Formel:
. Um den Flächeninhalt zu berechnen, verwenden Sie die Formel:
![]()
Setzen Sie die gegebenen Werte in die Formel ein:
![]()
Das Ergebnis der Berechnung ist:
![]()
Das bedeutet, dass ein Dreieck mit den gegebenen Maßen einen Flächeninhalt von ungefähr ![]() hat.
hat.
Beispiel 2: Berechnung des Flächeninhalts eines Dreiecks mit der Heron’schen Formel
Angenommen, Sie haben ein Dreieck mit den Seitenlängen ![]() cm,
cm, ![]() cm und
cm und ![]() cm. Die Heron’sche Formel kann verwendet werden, um den Flächeninhalt zu berechnen. Zuerst berechnen Sie den halben Umfang
cm. Die Heron’sche Formel kann verwendet werden, um den Flächeninhalt zu berechnen. Zuerst berechnen Sie den halben Umfang ![]() :
:
![]()
Dann setzen Sie die Werte in die Heron’sche Formel ein:
![]()
Das Ergebnis der Berechnung ist:
![]()
Das bedeutet, dass ein Dreieck mit den gegebenen Maßen einen Flächeninhalt von ungefähr ![]() hat.
hat.

Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)
Unsere Dienstleistungen:
-

Online Hausaufgabenhilfe in Mathe 1 Std.
100.00€ Add to cart -

Online Hausaufgabenhilfe in Physik 1 Std.
100.00€ Add to cart -

Online Nachhilfe in Mathe 11-13. Klasse 1 Std.
130.00€ Add to cart -

Online Nachhilfe in Mathe 5-10. Klasse 1 Std.
100.00€ Add to cart -

Online Nachhilfe in Physik 11-13. Klasse 1 Std.
130.00€ Add to cart -

Online Nachhilfe in Physik 5-10. Klasse 1 Std.
100.00€ Add to cart