Diesmal betrachten wir einen Würfel mal etwas genauer und zwar unter dem Gesichtspunkt Wahrscheinlichkeitsrechnung/Stochastik.
Erklären tun wir dies anhand einiger Beispiele mit passenden Zeichnungen. Diese sorgen für leichteres Verstehen.
Was genau ein Würfel ist, weiß eigentlich schon jedes Kind. Schon in den ersten Kinderspielen lernen wir diesen kennen. Der herkömmliche Würfel besteht aus sechs verschiedenen, gleich großen Seiten, diese sind mit den Zahlen von 1 bis 6 chronologisch beziffert.
Diese Beispielzeichnung zeigt den prinzipiellen Aufbau eines Würfels:
Ein Würfel anhand eines Baumdiagramms erklärt
Am Anfang wenden wir uns der Berechnung der Wahrscheinlichkeiten eines völlig normalen Würfels zu. Bei einem sechsseitigen Würfel ist die Wahrscheinlichkeit für alle Ziffern genau gleich.
Somit beträgt die Chance eine bestimmte Zahl zu würfeln, bei allen Zahlen 1/6. In der Mathematik stellen wir dies meistens in einem Baumdiagramm dar.
Dieses sieht bei einem Würfel mit sechs Seiten wie folgt aus:
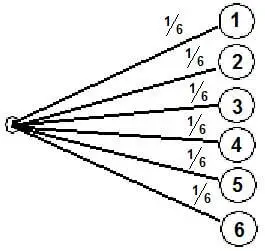
Aus der Grafik kann man entnehmen, dass es für für alle Zahlen die gleiche Wahrscheinlichkeit gibt, diese zu würfeln.
Verdeutlichen wir dies anhand folgender Beispiele:
1. Wie wahrscheinlich ist es eine 3 zu würfeln?
– Lösung: Die Möglichkeit eine 3 zu würfeln beträgt 1/6.
2. Wie wahrscheinlich ist es eine 2 zu würfeln?
– Lösung: Hier beträgt die Möglichkeit ebenfalls 1/6.
3. Wie wahrscheinlich ist es eine 1 oder 3 zu würfeln?
– Lösung: Bei der 1 beträgt die Möglichkeit 1/6, ebenso bei der 3. Das gewünschte Ergebnis stellen also zwei von sechs Seiten dar. Die Wahrscheinlichkeit beträgt somit 2/6.
4. Wie wahrscheinlich ist es mit einem Würfel eine gerade Zahl zu würfeln?
– Lösung: Gerade Zahlen sind die 2, 4 und 6. Es gibt also 3 Würfelseiten die mit einer geraden Zahl versehen sind. Die Möglichkeit diese zu würfeln beträgt somit 3/6.
5. Wie wahrscheinlich ist es mit einem Würfel eine ungerade Zahl zu würfeln?
– Lösung: Zu den ungeraden Zahlen zählen die 1, 3 und 5. Es gibt also 3 Würfelseiten die mit einer ungeraden Zahl versehen sind. Die Möglichkeit diese zu würfeln beträgt somit ebenfalls 3/6.
Kommen wir nun zu Beispielen, in denen der Würfel nicht nur einmal geworfen wird. Wie hoch wäre wohl die Wahrscheinlichkeit, zweimal hintereinander eine 6 zu würfeln? Oder andersrum zweimal hintereinander keine 3.
Für dieses Beispiel erweitern wir unser Baumdiagramm, um auch den zweiten Wurf abdecken zu können. Die zweite Stufe sieht somit aus wie die erste, da sich an unserem Würfel nichts ändert.
Wir stellen das Baumdiagramm aus Platzgründen etwas gekürzt dar.
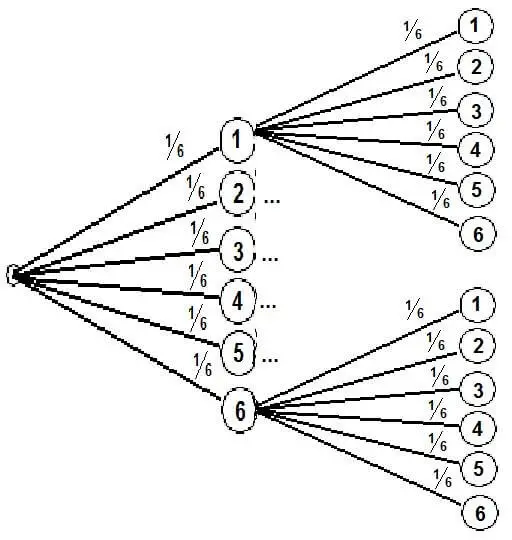
Um auf ein Ergebnis zu kommen, werden die Wahrscheinlichkeiten aus dem ersten Versuch, mit denen aus dem Zweiten multipliziert.
Dazu gibt es nun zwei Beispiele die dies verdeutlichen sollen:
1. Wie wahrscheinlich ist es zuerst eine 1 und danach eine 6 zu würfeln?
– Lösung: Die Möglichkeit auf Anhieb eine 1 zu würfeln liegt bei 1/6. Dies gilt auch für den Zweiten Versuch. Wird beides miteinander multipliziert erhält man eine Wahrscheinlichkeit von 1/6*1/6= 1/36.
2. Wie wahrscheinlich ist erst eine 6 und dann keine 3 zu würfeln?
– Lösung: Auch hier beträgt die Möglichkeit auf Anhieb eine 6 zu würfeln 1/6. Danach direkt keine 3 zu würfeln liegt bei 5/6. Das bedeutet, dass die Gesamtwahrscheinlichkeit bei 1/6*5/6= 5/36 liegt.
Hat Wirtschaftswissenschaften an der Universität Kassel studiert.
Einzelunternehmer seit Mai 2006 & Chefredakteur von mehreren Webseiten
Geschäftsführer & Gesellschafter der Immocado UG (haftungsbeschränkt)
